Many pedal steel guitarists view temperament as an issue of black or white: the instrument is tuned to just intonation (JI) or it is tuned to equal temperament(ET). Rather than argue over which is “correct”, most expert players agree that the tuning system used is simply a starting point. Your ears must be your guide to playing in tune.
With that simple fact in mind, I explored various tuning systems for the pedal steel, first on my F Diatonic copedent, and then on the more standard C6th. In the process, I discovered that a tuning system from the baroque era called meantone temperament (MT) actually works very well on the pedal steel. In this article, I will explain the theory behind meantone temperament and how it can be applied to the C6th copedent.
Doing the Math
Harmony is created by the intervals between notes. The size of intervals in measured in cents. There are 1200 cents in an octave. In ET, all of the intervals are even multiples of 100 cents. In JI, the intervals are not so evenly divided. The following chart shows the size of the three most important intervals, in cents:
| 3rd | 4th | 5th | |
|---|---|---|---|
| Interval in C |
C to E
|
C to F | C to G |
| Just Intonation |
386
|
498
|
702
|
| Equal Temperament |
400
|
500
|
700
|
| difference in cents |
-14
|
-2
|
+2
|
JI sounds very sweet and harmonious to the ear, but the math of JI doesn’t work out very well for some intervals on fixed pitch instruments. The following chart shows a problem with JI fifths, and how ET corrects it somewhat:
| Circle of Fifths | |||||
|---|---|---|---|---|---|
| note | C | G | D | A | E |
| JI |
0
|
+2
|
+4
|
+6
|
+8 |
| ET |
0
|
0
|
0
|
0
|
0
|
| MT |
0
|
-3.5
|
-7
|
-10.5
|
-14
|
Notice how stacking perfect 5ths in JI results in an E note that is way off the mark. If 386 cents is considered the sweetest sounding 3rd, 408 cents will be grossly out of tune to our ears. ET corrects it somewhat by shaving just 2 cents off the 5th, giving us a 3rd that is 14 cents sharp of the sweet spot.
The last line of the chart is an introduction to the theory of meantone temperament. If we trim the 5ths more than ET does, we get sweeter 3rds. The difference in the 4ths and 5ths is barely noticable, but the 3rds are much smoother. The amount of trimming required is evenly split among the four 5th intervals.
Applying Meantone Temperament to the C6th
A difference 3.5 cents on the circle of fifths will give you pure JI 3rds at the expense of the 4ths and 5ths. Through experimentation, I found that -2.5 cents is a very good compromise that’s easier to tune on an electronic tuner with 5 cent scale marks. The improvement from ET is very noticable, and it’s more “fault tolerant” than JI or the 3.5 cent meantone temperament.
On the C6th, I center the temperament on D to get a balance of notes on both sides of the tuner’s zero mark. Here’s a chart that shows how the math marches around the intervals:
| –> FOURTHS –> | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
G#
|
C#
|
F#
|
B
|
E
|
A
|
D |
G
|
C
|
F
|
Bb
|
Eb
|
Ab
|
|
-15
|
-12.5
|
-10
|
-7.5
|
-5
|
-2.5
|
0
|
+2.5
|
+5
|
+7.5
|
+10
|
+12.5
|
+15
|
| <– FIFTHS <– | ||||||||||||
Notice that the 3rds (C to E, for example) end up being 10 cents smaller than in equal temperament, resulting in a smoother blend of the tones. Moreover, it applies to all of the 3rds in the tuning. The 2.5 cent difference on the 4th and 5th intervals is barely noticable, and doesn’t sound out of tune at all.
Here’s how the 2.5 cent meantone temperament is applied to the standard C6th copedent:
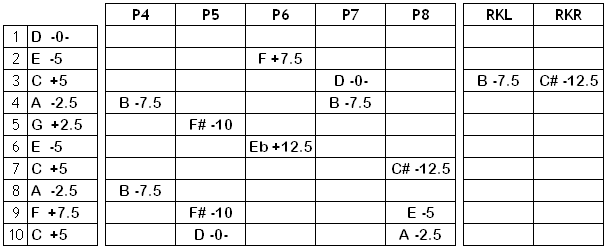
I’ve found this temperament to be easier to play in tune than ET, and as pleasing to the ear as JI. It’s systematic approach virtually guarantees that all 3rd, 4ths and 5ths will be nicely in tune. If you do the math you’ll discover that other intervals are equally acceptable. It’s close enough to ET to play with MIDI tracks or with any band, and it’s close enough to JI to please most players’ ears.
Other Issues
You may have noticed at the two ends of the calculation chart, that G# and Ab are two separate pitches. This is why meantone doesn’t work well on instruments that have 12 fixed pitches per octave. As you get into remote keys, more notes are needed. This is not a problem on pedal steel, because all of the notes of the remote keys are available with the same sweet intervals a fret above or below the more common keys.
As with JI, the bar must be placed slightly above or below the fret in some pedal positions to play in tune. The difference isn’t as pronounced as it is in JI, but playing right on the fret isn’t always in tune with other instruments. As with any tuning method, you have to learn to play it in tune. Your ears must be your guide to playing in tune.
A common question from steelers is “Can I use MT on the E9th?”. I don’t recommend it unless you have a guitar with no cabinet drop. The typical 5 cent drop from the E9th’s A+B pedals is enough to throw these calculations out of whack. There’s no pedal combination on the C6th that exerts that much stress on the machine. Maybe with an Emmons Counterforce or similar device, it would work. I haven’t tried it.
Music is an infinite study. What a bland world it would be if there really were, as some theorists suggest, only 12 musical pitches per octave. In truth there are an infinite number of pitches that can be combined in an infinite number of ways. These things were discovered centuries ago, but they are only now being applied to the pedal steel. Don’t limit yourself with musical dogma. Explore the world of music freely, and keep on steelin’.
Copyright ©2005 by Bob Lee
Bob, very interesting stuff. I’ve been trying to get my head around the various meantone systems on and off for quite a while. I understand the goal of having major thirds that are closer to a ‘pure’ 5:4 interval by shrinking the 5ths a few cents. What I don’t understand about this system outlined above is that the 3rds built on B, F# and C# are not in tune. Of course, in the practical application of tuning the changes on the C6 copedant, it works well because there are no major 3rds in the copedant tuned to B, F# or C#. And I understand the notion of a ‘wolf tone’ that is unusable, and I would assume the Ab (vs G#) is just that, as you outlined in the description. Are these extra unusable thirds built on B, F# and C# related to the subdivision of the comma that results in systems such as 1/4 comma, 1/6 comma and so on? I would imagine the key thing here is that the system doesn’t cover all intervals and the trick is to ‘rotate’ one’s tuning system to avoid these undesirable intervals.
As you noted:
B to D# – there is no way to play that interval on open strings.
F# to A# – there is no A# in the C6th copedent. Many people have an A to Bb lever, which must be avoided when using p5 to get an F#. Bb is a higher note than A#.
C# to E# – again, there is no E# in the copedent. You do have to avoid the C# to F on strings 3 and 2, as it’s too wide to be a usable major 3rd.
There are intervals that are not possible on the open strings, but when playing up the neck those intervals can be easily found just a fret away. For example, anywhere that you have a F to A major third, F# to A# is just one fret higher.
I find meantone to be suitable for the music I play, which is fairly standard mid-century swing, country, blues, and Hawaiian. People who are into really complex chords should probably use equal temperament. Emmons did.
Emmons used “sweetened” tuning on both E9 and C6
At the end of the day, it’s all about your ears!