Music,
Evolved By Intuition,
Described By Science
|
|
by Ed Packard
|
|
Some years ago, a close friend from the "teen" years and I had a reunion
of sorts. After dinner he showed me a guitar that his wife had bought him.
We used it to trip down memory lane, and then he played a simple C chord at
the nut position and asked me "why does that sound good?". My friend, Walter
Hicks, Ph.D. in plasma physics, Bachelor and Master degrees received on the
same day, in Electrical Engineering, and from MIT, had asked a very simple
question. Because of his background, I did not think that he was asking for
answers like, ..It is a nice sounding guitar, ..You have your fingers
correctly placed, ..The instrument is in tune, etc.; He was asking for an
answer related to his background and training, ..an answer that might start
"qualitatively," but could lead to "quantifying" the reason for the goodness
of the sound. How would you have answered the question?
|
|
I took the guitar and fooled around for a minute, and then said to Walt,
"It must have something to do with the harmonic relationships (meaning the
frequency relationships) of the strings to each other.". I had been playing
around with the "chimes," but not as well as Lenny Breau would have done.
The session ended, and I went to the airplane.
|
|
On the plane, I took out my HP41C calculator, and started to run some
equations re string vibration and harmonics. An exciting pattern began to
appear. When I got home I fired up the computer, and increased the scope of
my investigation; Here is the result of the "simple question" my "not so
simple" friend asked.
|
|
I chose a single string, and assumed a fundamental frequency, say 440 for
an A string, and proceeded to calculate the first thirty-two harmonics. Next,
these values were converted back to the equivalent musical notes. Then I
calculated the values of the frequencies for each fret on the A string. From
these simple calculations, a great insight dawned. This insight can be masked
by the values of the "A" string calculations, and the "A" scales sharps, so
we will reduce the "noise" by assuming a string with a fundamental frequency
of 1, and assigning it the label of a "C" note, so that we may talk in the
key of "C".
|
|
A string will vibrate at frequencies that are integer (whole
number) multiples of the string's fundamental.
|
|
If the string's fundamental (call it h1) is 1, then h2 is 2x1, h3 is 3x1,
etc.; The harmonic string calculations gave the values for h1 through h32.
In our simplified case wherein h1 = 1 unit of frequency, or if you prefer,
1 cycle per second, h1 = 1 cycle and h32 = 32 cycles. The string was
vibrating at all these frequencies, and more, at the same time.
|
|
An increase of an "octave" (say from C1 to C2) is an increase in frequency
of 2xC1, The frequency of the next octave is 2xC2, or 4xC1. All of the
"binary" numbers (1,2,4,8,16,32 etc.) are then "C" notes. Why not, ..this
is a "C" string. What about the other integers (3,5,6,7,9,10,11,12,13,etc.),
they are not "C" notes. By reducing the h1 frequency value to 1, the pattern
almost leaps from the page, as compared to the mass of figures that was the
result of the A 440 calculations. Can you see it yet?
|
|
The folk that speak "intervalese" should land on it with little problem,
..particularly since I stopped the non octave integers at 13. The note
equivalent of the values are h1 = C1, or "root"; h2 = C2, octave, or #7th;
h3 = G, or 5th; h4 = another octave; h5 = E, or 3rd; h6 is a binary of h3,
and is therefore a 5th in a different octave; h7 is roughly a 7th (h7 is
really b7th, h15 is 7th); h9 is roughly a 9th; h10 is a binary of h5, so it
is another 3rd; h11 is roughly an 11th; h12 is a binary of h3 and h6, hence
it is another 5th; h13 is roughly a 13th. And the beat goes on! If we swap
h3 and h5, we have the "odd" intervals of the major (Ionian) scale (in this
case the C major scale) as we would call them in the first two octaves above
the root. If we move the 9th, 11th, and 13th intervals down into the first
octave, they become the "even" intervals (2nd, 4th, and 6th), and we have
the complete "diatonic" scale. The actual vibrational frequencies are not
in the first two octaves (except for h1 and h2), but they are the right
intervals and notes.
|
|
The "loudest" vibration is h1, the Root. the next loudest is h2, the next
loudest is h3 etc. The first "singing" was probably a line of single notes
(frequencies). The first "harmonies" were probably octave related. The next
development in harmony was probably 5ths. The next was probably 3rds. The
development of the most dominant scale (major), and the most used chords,
appears to be related to the notes found in a single vibrating string. Over
time, and with familiarity, our taste in chord complexity moves beyond the
three, and four tone variety. Our taste in progressions also become more
complicated. We make room for the Duke Ellingtons, the Billy Strayhorns,
the Stan Kentons, and their descendants in our musical world.
|
|
Chords are (by observation) composed of the "odd" numbered intervals of the two octave scale. The "C" chord (three tone) is composed of the notes C,E,G, ..or Root, 3rd, and 5th, ..or h1, h5, and h3. If we had to leave out a note, we would probably choose to drop the 3rds, ..It's presence in the single vibrating string is weaker than the 5ths, and it is harder to "tune" as we shall see.
|
|
The first four tone chord would be Root, 3rd, 5th, 7th, or in C, Cmajor7, ..and so on up through the seven tone chord which would be a major 13th, or in the C scale, CM13. The notes in the single vibrating string's harmonics demand reinforcement by sympathetic vibrations from adjacent strings, and that to the degree of the loudness of that notes presence in the single vibrating string. The music rules (what and how) arrived (evolved) before the understanding of the "why" in physics terms. In a sense, it was much harder to discover a self consistent description than to produce the music itself. The mind is a magnificent electro chemical device. We get to carry it around, but we do not control or understand it. The musical mind responded to the patterns of vibrating strings, blown pipes (same principle), hollow logs, and stretched animal skins, before we saw the patterns involved. GOD CREATES, MAN ARRANGES, SCIENCE EXPLAINS; Explaining is just another form of "arranging".
|
|
In the patterns described above, you will see the foundation for the TWO OCTAVE, SEVEN TONE CHORD structure in the "13 series" pedal steel guitar. If there is an interest expressed, we can go on to the issues of "tuning difficulties," chord structure, why we like the chord progressions that we do, modal scales, and more, ..It all may be described in the context of the above insight. If we understand why we like what we like, then we can have more of it more quickly, and with less effort. Once we "see" the pieces, we can spend more time "arranging" them. It beats playing by the numbers for some folk, but not for all.
|
|
It is easier to visualize the foregoing information as a diagram, so here it is in table form. h is the harmonic #, Int 1 is the interval in the first octave of the two octave system, Int 2 is the interval in the second octave of the two octave system, Note is what the alpha name of the note would be in the C scale, and Oct# tells the octave #, with respect to h1, in which the notes and intervals would be found. The amplitude of the harmonic in the single vibrating string decreases with increasing harmonic #.
|
|
|
TABLE #1,
harmonics in a single vibrating string,
in order of increasing harmonic #
| | | | | | |
| | | | | | |
| h1 | h2 | h3 | h4 | h5 | h6 | h7 | h8 | h9 | h10 | h11 | h12 | h13 |
|---|
| Int 1 | 1 | 1 | 5 | 1 | 3 | 5 | b7 | 1 | 2 | 3 | 4 | 5 | 6 |
| Int 2 | #7 | #7 | b13 | #7 | b11 | b13 | #13 | #7 | 9 | b11 | 11 | b13 | 13 |
| Note | C | C | G | C | E | G | Bb | C | D | E | F | G | A |
| Oct# | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 |
|
|
|
TABLE #2,
harmonics in a single vibrating string,
in order of increasing chord complexity
| | | | | | |
| | | | | | |
| h1 | h2 | h4 | h8 | h5 | h10 | h3 | h6 | h12 | h15 | h9 | h11 | h13 |
|---|
| Int# | 1 | 1 | 1 | 1 | 3 | 3 | 5 | 5 | 5 | 7 | 9 | 11 | 13 |
|---|
| Note | C | C | C | C | E | E | G | G | G | B | D | F | A |
|---|
| Oct# | 1 | 2 | 3 | 4 | 3 | 4 | 2 | 3 | 4 | 4 | 4 | 4 | 4 |
|---|
|
|
|
|
Notice the binary relationship of h1 through h8, h5 to h10, and h3 through
h12. Now that we see the pattern, it is easy to predict that h16, h32, and
h64 would be Roots (1's); h24, h48, and h96 would be 5ths; h15, h30, and h60
would be 7ths; h18, h36, etc., would be 9ths; h22, h44, h66 etc., would be
11ths; And h26, h52, etc., would be 13ths. Nature has led us, via the route
of intuition, into ever more complex musical patterns; Now that we can
visualize the existing and accepted patterns by using the common language of
letters and numbers, what hinders us from taking a peek into the future?
Before we do that, lets work a bit more on the present possibilities. Table
#3 shows how the odd intervals of the 2nd octave become the even intervals of
the first octave, and provide us with the "diatonic" scale, ..our famous do,
re, mi, scale.
|
|
|
TABLE #3, harmonics in a single vibrating string, in order of the
one octave diatonic scale
| | | | | | |
| | | | | | |
| h1 | h2 | h4 | h8 | h9 | h5 | h10 | h11 | h3 | h6 | h12 | h13 | h15 |
|---|
| Int# | 1 | 1 | 1 | 1 | 2,9 | 3 | 3 | 4,11 | 5 | 5 | 5 | 6,13 | 7 |
|---|
| Note | C | C | C | C | D | E | E | F | G | G | G | A | B |
|---|
| Oct# | 1 | 2 | 3 | 4 | 4 | 3 | 4 | 4 | 2 | 3 | 4 | 4 | 4 |
|---|
|
|
|
|
Meanwhile, back in Boston, many years ago, Walt and I went swimming in the
MIT pool . We did this every Tuesday and Thursday night. Tuesday and Thursday
nights were coed nights, ..this was the "liberal arts" part of an MIT
education. One Thursday night Walt did not show up. The next day I asked
him why he had missed the session. His answer was that he had to take a
final. Oh, a day class switched to a night final?, .."No". A class from
another night switched to a Thursday final?, .."No, I had a class on Tuesday
and Thursday evening". But Walt, you have been at the pool every Tuesday
and Thursday night. "Ed, I missed a Tuesday to sign up for the class". Walt,
what was the class? Maybe something difficult, like underwater basket weaving?
"No, it was "tensor calculus". Gasp! How did you feel about the exam? "Fine".
Walt, how can you do that? "Ed, I have a "plug in" system for mathematics".
As I recall, Walt came in about 3rd in the class on the exam.
|
|
The point is that Walt recognized the patterns of the subject where others
had to be shown the details. His mind worried about "why" as opposed to "what"
and "how". Once he saw the principle, he could derive the function. All of
these things are "patterns"; Music is patterns; The string's behavior is
patterns; The fret placement is patterns. Nature has provided them to us
like a giant puzzle, all we need to do is find the pieces and fit them
together; And so we go back to the arithmetic of music; We will try to
avoid using tensor calculus, ..I don't really understand the stuff anyway.
|
|
So far we have shown the relationship between the frequencies found in a
single vibrating string, and the two octave odd interval scale upon which
chords are based. Further, we have shown how folding the second octave
into the first octave produces the diatonic scale. These patterns have
been used to point out the reason why music has come to where it is, later
we will try to show where music may go in the future.
|
|
To get to the present point in our path, we have taken a Root frequency,
normalized it to 1, multiplied it by the integers 1 through 13 to get the
basic harmonics found in the vibrating string, shown the binary relationship
of octaves, and used these bits of information to develop a few scales.
Now we will proceed to get a bit picky, and reduce these to string lengths
and fret boards.
|
|
When a string of a given material, diameter, and length is placed under
tension and plucked it vibrates. In music, we call the string by an "alpha"
name associated with the fundamental vibrating frequency (h1) of the string.
These are names like C, C#, Db, etc., names of musical notes. Numerals may
be placed after these note names to designate their position in the audible
frequency spectrum, ..C1, C2, C3, and so forth. The frequency of C2 is twice
that of C1, ..the frequency of C3 is twice that of C2, and four times that
of C1. In our development of charts 1, 2, and 3, we decided to "normalize
the frequency of our "C1" note to 1. As a result, the frequencies of the
harmonics became 1,2,3,4, and so on through 13. The names of these
"normalized frequencies appeared to agree with the names of the odd
intervals in the two octave seven tone chord designation system with two
exceptions, ..3, and 5. h3 was the 5th, and h5 was the 3rd. In the development
of the above charts, we continued to refer to the notes by their harmonic
series number, even when we reduced their musical order to a single octave,
Now that we know where they came from, let's give them normalized values
for the octave for the octave into which we have placed them.
|
|
We gave a value of 1 to C1, h2 became C1x2. h3 became C1X3. C1x3 is not C,
it is G. The frequency of our G may be moved up an octave by doubling it,
or down an octave by halving it. If we halve the frequency of C1x3 = G = 3,
we get G = 1.5; The frequency of G will always be 1.5 times the frequency of
the next lowest C note. If we apply this move to C1x5 = E = 5, we get E = 5/2
or 2.5, and if we do it again to get into the same octave as C1, we get
E = 2.5/2, or E = 1.25; The frequency of E will always be 1.25 times the
frequency of the next lowest C note. In general terms, the frequency of the
3rd is 1.25 times that of the Root, and the frequency of the fifth is always
1.5 times that of the Root. This is true for our harmonic series. Since we
have the diatonic scale (table #3) with harmonic numbers intact, lets make
table #4 by applying the above technique to the harmonic numbers, which are
our frequency values (because we "normalized" C1 to 1, and with the exception
of h3 and h5 are our interval numbers. We will label the data as "Hz#1.
|
|
The result looks like this:
|
|
|
|
|
TABLE #4, normalized frequencies in a single vibrating string,
for a one octave diatonic scale
| | | | | | |
| | | | | | |
| h1 | h2 | h4 | h8 | h9 | h5 | h10 | h11 | h3 | h6 | h12 | h13 | h15 |
|---|
| Int# |
1 | 1 | 1 | 1 | 2,9 | 3 | 3 |
4,11 | 5 | 5 | 5 | 6,13 | 7 |
|---|
| Note |
C | C | C | C | D | E | E |
F | G | G | G | A | B |
|---|
| Oct# |
1 | 2 | 3 | 4 | 4 | 3 | 4 |
4 | 2 | 3 | 4 | 4 | 4 |
|---|
| Hz#1 |
1 | 1 | 1 | 1 | 1 | 1.25 | 1.25 |
1.375 | 1.5 | 1.5 | 1.5 | 1.625 | 1.875 |
|---|
|
|
|
|
Our table has too many C's, E's, G's ; Lets reduce it to straight do, re, mi, for one octave.
|
|
|
TABLE #5, one octave diatonic scale with frequency ratios from harmonic series
|
| | | |
| | | |
| Solfeggio |
DO | RE | MI | FA |
SOL | LA | TI | DO |
|---|
| Interval |
Root | 2nd | 3rd | 4th |
5th | 6th | 7th | Oct |
|---|
| Note |
C1 | D1 | E1 | F1 |
G1 | A1 | B1 | C2 |
|---|
| Hz #1 |
1.0 | 1.125 | 1.25 | 1.375 |
1.5 | 1.625 | 1.875 | 2.0 |
|---|
|
|
|
|
If C1 is the open string, then C2 is the string at 1/2 the open string length;
halve the string length, double the frequency, ..double the frequency, go up
an octave. We have arrived at fret #12. We have used up half of the neck
(string) length. if we go to C3, we will be at fret #24, and will have used up
another 1/2 of the remaining string length. It looks like our Hz #1 values are
related to string length; 1/1 = 1, or the whole string length; 1/2 = 0.5, or
1/2 the string length; C3 would have a frequency of 4 x C1 = 4, .1/4 =0.25,
or 1/4 the string length, and so on. We simply take the reciprocal of the
frequency ratio of the desired note to the open string frequency (ratio
value divided into 1) and we have the location of that note on the neck.
|
|
We will pick an easy neck length, say 24 inches, and add the results to the
table. While we are modifying the table, we might as well add the flats and
sharps for the chromatic scale; It will show us where we need more information
to fill out the frequencies between diatonic notes, and the distance between
frets.
|
|
Because of the amount of information per table cell, we will change the shape
of the table. The new format will have the low notes at the bottom of the
table.
|
|
|
TABLE #6, one octave chromatic scale with ratios, differences,
and fret location for a 24" neck
|
|
|
|
|
|
|
|
|
Int |
Note |
h Series ratio |
Constant ratio |
C as % of h |
Cents Diff. |
Fret Calc from C |
|---|
| DO |
Oct |
C |
2.000 |
2 |
100.000 |
0 |
12.000 |
| TI |
7 |
B |
1.875 |
1.8877 |
100.680 |
-0.67993 |
11.286 |
|
b7 |
A#-Bb |
1.750 |
1.7818 |
101.817 |
-1.817 |
10.530 |
| LA |
6 |
A |
1.625 |
1.6818 |
103.495 |
-3.49494 |
9.730 |
|
#5 |
G#-Ab |
1.5625 |
1.5874 |
101.594 |
-1.59367 |
8.881 |
| SOL |
5 |
G |
1.500 |
1.4983 |
99.887 |
0.112862 |
7.982 |
|
b5 |
F#-Gb |
1.4375 |
1.4142 |
98.380 |
1.619926 |
7.029 |
| FA |
4 |
F |
1.375 |
1.3348 |
97.079 |
2.920738 |
6.020 |
| MI |
3 |
E |
1.250 |
1.2599 |
100.794 |
-0.79368 |
4.951 |
|
b3 |
D#-Eb |
1.1875 |
1.1892 |
100.144 |
-0.14376 |
3.818 |
| RE |
2 |
D |
1.125 |
1.1225 |
99.774 |
0.225596 |
2.618 |
|
b2 |
C#-Db |
1.0625 |
1.0595 |
99.714 |
0.285826 |
1.347 |
| DO |
Root |
C |
1.000 |
1.0000 |
100.000 |
0 |
0.000 |
|
|
|
READ THIS CHART BOTTOM UP, just like you were reading tablature.
- The "Int" column gives the intervals in the the terms most often used
in chords, i.e. b3 as opposed to #2.
- The "Note" column uses the convention that D# = Eb and so forth,
..a convenience.
- The "h series ratio" values in this column are taken from higher h#'s
than previously used in order to get the sharps and flats values.
- The "Constant ratio" values give the constant rate of change in
the distance between frets, and the rate of change in frequency as a
function of adjacent halftones.
- The "C as a % of h" column gives the difference between the previous
two columns as a percentage.
- The "Cents difference" column gives the difference between the h
derived values, and the Constant derived values in cents. A cent
is 1/100th of the frequency difference between adjacent halftones.
- The "Fret calc from C" column gives the distance in inches for each
fret in the first octave of a 24 inch neck.
|
|
|
|
You will notice that there is a difference in value between the Constants
ratio column and the h ratios column. This difference is part of the "tuning"
problem, the rules for which seem to change for steel players every decade or
so. The magic constant is related to "the twelfth root of two", and is applied
to break the octave, and the neck up into distances and frequencies having a
constant percentage of change as a function of increasing (or decreasing)
halftones. The basic value for increasing halftones is 1.05946309 (about),
..one over that for the decreasing halftones. This value also gives the amount
of tension change required to raise a string by a halftone; It is a
multiplier.
|
|
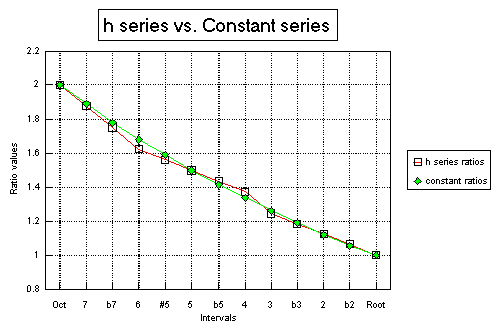
It assists understanding to see differences in plotted form. Graph #1 shows
both the h series data, and the Constant series data plotted as a function of
interval.
|
|
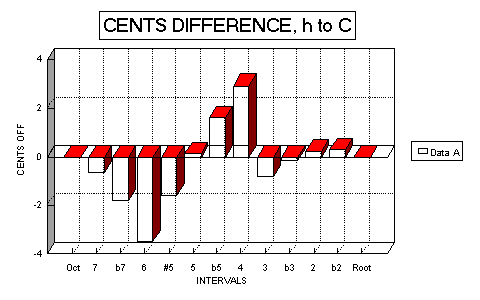
Graph #2 shows the Cents difference between the two series plotted against
intervals.
|
|
|
|
|
GRAPH #1 - Note that the Root, Octave, and 5th agree,
while the 6th and the 4th disagree most.
|
|
|
|
|
GRAPH #2
|
|
|

